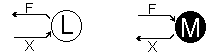
La synthèse modale est une approche de la synthèse par modèles physiques différente du paradigme à masses et ressorts. Elle est fondée sur deux contraintes primordiales, afférentes au dispositif de contrôle et à la qualité sonore, qui ont motivé l'utilisation du formalisme modal. Ces contraintes sont d'une part de pouvoir appliquer aux modèles de simulation tous les gestes instrumentaux présents dans les modes de jeu d'instruments traditionnels et d'autre part d'obtenir un son le plus proche possible de son modèle acoustique. Dans un contexte musical, il est évident que ces deux contraintes sont nécessaires mais pas suffisantes. En effet, toute technique de synthèse doit pouvoir offrir au compositeur, non seulement la possibilité de simuler des sons existants, mais aussi et surtout de pouvoir effectuer des transgressions et des dépassements des modèles établis. Ainsi, les programmes de simulation doivent posséder une capacité d'extension des possibilités naturelles des instruments, au niveau des contrôles mais aussi de la construction même des structures instrumentales. Les extensions ne sont possibles que si les structures possèdent flexibilité et modularité, une homogénéité de représentation de toutes les structures vibrantes est donc indispensable, permettant ainsi d'accroître, par assemblage, les possibilités d'utilisation des modèles. De plus, pour une efficacité optimale, il est nécessaire de minimiser le coût informatique en temps de calcul et en complexité algorithmique.
Comme l'explique F. Crawford, un système complexe peut-être découpé en éléments simples qui ont les mêmes propriétés que l'ensemble : c'est là la base même de la synthèse modale.
" Le mouvement d’un système compliqué comportant de nombreuses parties mobiles peut toujours être vu comme composé de mouvements plus simples, appelés modes, qui ont lieu tous à la fois. Quelle que soit la complexité du système, on s’aperçoit que chacun de ses modes a des propriétés très semblables à celles d’un oscillateur harmonique simple19 ".
L’objet est donc représenté comme un ensemble de sous-structures vibrantes dont le nombre est bien moins important que celui des masses et des ressorts. Ces sous-structures sont des cordes, des embouchures, des tubes, des archets, etc. qui réagissent à des excitations extérieures (souffle d’air, frappe…). La synthèse modale définit chaque sous-structure grâce à un ensemble d’informations dites données modales. Ces données modales sont un ensemble de coordonnées représentant la forme des modes vibratoires20 de l’objet, ainsi que les fréquences et coefficients d’amortissement de ses modes de résonance. Ainsi, les équations décrivant l’objet, ne représentent pas l’objet lui-même mais la façon dont il est susceptible de vibrer. " La vibration totale instantanée d’un instrument est donc exprimée comme la somme des contributions de ces modes21 ".
Dans le cas ou les sous-structures vibrantes sont simples, les données modales sont obtenues sous forme d’équations dans les traités théoriques de mécanique. Si, ces structures sont complexes, les données sont découvertes par expérimentation sur des instruments réels. Le facteur favorable à la synthèse modale est que les chercheurs disposent déjà d’une méthodologie d’analyse des modes vibratoires, qui a de nombreuses applications industrielles et peut être utilisée pour la synthèse du son, et d’outils pour ce genre d’analyse mécanique comme des transducteurs22 et des logiciels d’analyse.
La synthèse modale est plus souple que la technique à masses et ressorts. En effet, il est par exemple possible d’ajouter ou de supprimer des sous-structures dans le temps (pour simuler le changement de taille d’un instrument en cours de jeu) ou bien de faire des interpolations entre deux instruments en combinant les sous-structures de façon non-naturelle, etc.
La synthèse modale fut découverte en 1979 par l’équipe de l’ACROE23 qui l’inclut dans le système Cordis-Anima. En 1989, Jean-Marie Adrien a utilisé et développé cette technique qui fut ensuite la base du logiciel MOSAÏC, développé par l’IRCAM.
Mosaïc a aujourd’hui évolué et a été renommé Modalys (pour éviter toute confusion avec le navigateur Internet, Mosaïc). Pourtant c’est Mosaïc que nous décriront plus en détail par la suite, premièrement parce qu’il est plus aisé de comprendre le principe de cette technique à travers cette version plus simple du programme, et deuxièmement parce que des compositeurs, comme Kaija Saariaho dans Amers24, ont utilisé ce programme sous cette forme ancienne. Evidemment, nous n’omettrons pas de montrer en quoi Modalys représente une amélioration de MOSAÏC et quels sont les perfectionnements que les équipes de l’IRCAM mettent au point actuellement.
Mais avant de décrire ce système développé à l’IRCAM, nous commencerons, dans l’ordre chronologique par présenter Cordis-Anima.
CORDIS-ANIMA est un système de modélisation et de simulation d’objets physiques en temps réel, basé sur la simulation de structures vibrantes à partir de mécanismes élémentaires. Ces objets sont visibles, audibles et manipulables (des informations gestuelles peuvent être envoyées de l’opérateur vers l’objet mais également de l’objet vers l’opérateur, grâce à des interfaces tactiles à retour d’effort). Développé par l’ACROE depuis 1978, par Claude Cadoz, Annie Luciani et Jean Loup Florens, ce programme constitue un outil informatique pour la création musicale et la création d’images animées. CORDIS est dédié à cette première fonction et ANIMA à la seconde, mais les deux ont en commun une base matérielle et conceptuelle importante. Le but de CORDIS-ANIMA est de produire des répliques virtuelles d’objets du monde réel, et de permettre une simulation totale des phénomènes produits par l’objet, mais aussi une simulation de l’objet lui-même.
Pour réaliser la simulation d’un objet physique, il est nécessaire de connaître, parmi ses attributs et propriétés, ceux qui ont une incidence sur la production et le contrôle des phénomènes sensibles. Il faut ensuite que cette connaissance permette de réaliser un programme qui produira la simulation. Le modèle joue le rôle d’un intermédiaire permettant de décrire et caractériser les connaissances utiles. CORDIS-ANIMA a pour première fonction de nous permettre de réaliser ce modèle. Les modules et les fonctions utilisés, sont les éléments même de la modélisation mais aussi ceux de la simulation, en effet, CORDIS-ANIMA est également un système d’algorithmes élémentaires de simulation.
CORDIS-ANIMA permet de décrire puis reconstruire des objets à l’intérieur de l’espace virtuel de simulation. Il permet également de construire des objets qui n’ont pas d’équivalent dans le monde réel. En cela, CORDIS-ANIMA est un langage et comme tout langage : un moyen de création.
Le formalisme général de CORDIS-ANIMA est issu de deux impératifs initiaux, l’un matériel : la nécessaire discrétisation et la finitude des communications entre l’ordinateur et l’univers réel. L’autre résulte d’un choix : c’est celui de la modularité et surtout de " l’experimentabilité " ou de la " physicalité " des modules.
La simulation d’un objet n’a d’intérêt que si une communication sensible est établie entre l’opérateur et cet objet. Cependant, cette simulation est établie grâce à l’ordinateur et toute communication devra être réduite à des courants électriques, c’est à dire des signaux uni- voire multidimensionnels en nombre limité. Il en résulte une contrainte dans les processus de communication : la communication entre l’opérateur et le modèle ainsi que la communication entre les éléments de l’objet simulé, devront être discrètes et de dimension finie. Toute communication devra donc être idéalisée et représentée sous forme d’un message mécanique ponctuel.
Dans la réalité, les communications entre objets physiques sont non-orientées et font intervenir deux variables duales : l’une intensive (une force ou une intensité F), l’autre extensive (un déplacement ou une déformation X). Or la communication entre les objets simulés est forcement unilatérale, c’est à dire à un seul sens : entrée ou sortie. On est donc contraint de représenter toute communication sous forme bidirectionnelle, grâce à des paires indissociables d’entrées et sorties. On est donc amené à séparer les deux variables duales et à les affecter aux deux éléments de la paire. On obtient alors deux situations possibles : soit on a une force en entrée et une position en sortie, on appelle M ce point de communication, soit on a la situation inverse et l’on nomme L ce deuxième point de communication (voir Figure 8). Ces deux types de points constitueront la base du formalisme CORDIS-ANIMA.
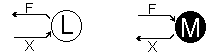
Figure 8 : Représentation des points L et M.
La construction d’un objet à partir de ces éléments de base L et M se fait en établissant un lien entre eux. Ce lien est un échange d’informations qui se fait par les entrées et sorties des points M et L (voir Figure 9). Ainsi, un point M peut recevoir les sorties de force de plusieurs points L : il reçoit, en entrée, une force dont la valeur est égale à la somme des forces de sortie des points L (voir Figure 10). Par contre, un point L ne peut recevoir qu’une sortie de position d’un point M, car il n’existe aucun moyen, ayant un sens physique, qui permet de combiner plusieurs positions différentes. Il va de soi que deux points M ou deux points L ne peuvent être connectés ensembles.
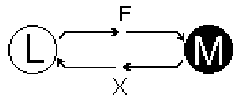
Figure 9 : Connexion d’un point L avec un point M.
Figure 10 : Connexion d’un point M avec plusieurs points L.
L’ensemble de ces points, connectés entre eux, forme un réseau. La structure obtenue peut être unidimensionnelle, bidimentionnelle voire tridimensionnelle. Les variables circulant par les points de communication peuvent être les coordonnées d’un point ou les composantes de force sur un axe, dans un plan ou dans l’espace. Des interfaces (ou transducteurs) permettant un contact sensible entre l’opérateur et l’objet simulé sont également représentées dans l’objet complet. On leur associe des modules spécifiques chargés d’évoquer leur présence, et leurs liaisons avec le reste des constituants de l’objet permettent la circulation des informations venant de l’objet lui-même ou de l’opérateur. Lorsqu’on parle de la partie purement numérique de l’objet, on parle d’objet interne.
Le principe de combinaison des modules exposé ci-dessus, permet une certaine généricité, c’est à dire la possibilité de construire, à partir d’un ensemble limité d’éléments différents, une grande variété d’objets. CORDIS-ANIMA tient son fondement même dans le fait que les modules constituant l’objet, sont de même nature que l’objet. Cela signifie que tous les modules formant l’objet simulé, même s’ils ne correspondent à aucun objet existant, ont une réalité physique expérimentale et sont accessibles à nos sens. Un objet global est alors un ensemble de sous-objets entre lesquels sont établies des communications spécifiques de même nature qu’entre l’opérateur et l’objet global. Néanmoins, pour former des objets complexes, un autre type de liaison est nécessaire : une liaison fixe entre deux points L, car toute autre liaison ne permettrait que des figures limitées (voir Figure 11 et Figure 12).
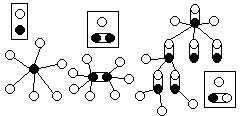
Figure 11 : Types de liaisons induisant des figures limitées.
Figure 12 : Liaison permettant toutes les figures possibles.
Les points M jouent donc le rôle de grains de matière, positionnés dans un espace tridimensionnel (ou plus simplement bi- ou unidimensionnel), alors que les points L tiennent le rôle d’éléments de liaison, calculant les forces agissant entre ces points. Il ressort de ce cadre formel que la simulation numérique nous impose une discrètisation des éléments physiques et des communications qui ont lieu entre eux ainsi qu’entre l’opérateur et l’un d’eux. L’art de la simulation est de jouer avec notre propre système de perception pour nous donner l’impression d’un phénomène continu.
En dehors des modules physiques formés de points L et M, un autre type de module est employé pour permettre la formation d’objets complexes. Ces modules fonctionnels qui ne manipulent pas uniquement des variables physiques et ne répondent pas obligatoirement à un modèle physique immédiat sont utilisés aux côtés des autres modules et permettent d’étendre considérablement les possibilités de représentation. Le nombre de ces modules fonctionnel est très important et l’opérateur peut aussi, s’il le désire, en créer de nouveaux, je n’en décrirai donc que trois qui sont les plus utilisés et qui permettent de comprendre en quoi ils augmentent les possibilités de simulations.
Les modules de variation structurelle dynamique ont pour fonction de faire passer l’objet d’un réseau d’interconnexions entre ses composants à un autre, durant la simulation. Ces modules possèdent, comme les objets, un ou plusieurs points de connexion. Ils possèdent également des sorties logiques, dont les valeurs sont booléennes et qui permettent, en fonction des ordres donnés d’établir ou non les connexions. L’action d’un de ces modules de variation structurelle dynamique peut être déclenchée par une variation interne de l’objet auquel il est connecté ou bien provoquée par l’intervention de l’opérateur.
Les modules de variation paramétrique dynamique n’agissent pas sur la structure de l’objet mais sur la valeur de ses paramètres pendant la simulation (plus précisément sur les paramètres de l’algorithme qui définit cet objet). Pour chaque objet, tous les paramètres sont modifiables, par l’opérateur ou par l’objet lui-même, en dehors du temps de la simulation ; mais seuls certains paramètres25, choisis à l’avance, sont modifiables pendant la simulation grâce à ces modules fonctionnels. Par exemple, ceci permet de faire grossir un gong pendant sa résonance pour obtenir un effet de glissando (effet employé par Kaija Saariaho dans Amers).
Les modules de changement de point de vue relatif permettent de changer la " taille " relative des objets entre eux ou par rapport à l’opérateur. Lors de la modélisation d’un objet, il est évident qu’un rapport d’échelle doit être établi entre les parties de l’objet mais également entre l’opérateur et cet objet. Ce module fonctionnel permet de changer ce rapport d’échelle, ce qui peut donner la sensation à l’opérateur que l’objet ou une de ses parties change de taille. Ce module se place entre deux sous-structures déjà définies et agit à la manière d’un " convertisseur " avec des facteurs multiplicatifs. Il permet de changer l’échelle des informations, des variables, forces et déplacements avant de les associer à leurs transducteurs respectifs. Ce module fonctionnel peut être également utilisé pour distribuer la variable " sortant " d’un module aux entrées de plusieurs autres modules (voir Figure 13).
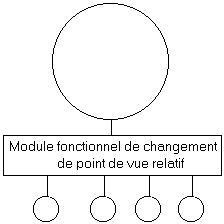
Figure 13 : Connexion d’un module aux entrées de plusieurs autres modules.
Ce sont les systèmes d’algorithmes qui vont permettre de calculer les différents états de l’objet dans le temps. C’est eux qui constituent la simulation en elle-même. Les principes énoncés précédemment ne constituent que le cadre formel de cette simulation. Le défi à relever est de construire ces algorithmes uniquement à partir des atomes, points matériels et éléments de liaison, et de trouver le meilleur principe d’économie à chaque niveau de cette construction. Pour établir ces algorithmes on peut traduire en équations physiques les comportements de l’instrument ou de l’objet réel étudié. " L’algorithme est, en quelque sorte, la vérification de l’équation ainsi transposée en temps et espace discrets et variables quantifiées, pour toutes les valeurs (discrètes) consécutives du temps26 ". L’inconvénient de cette méthode c’est que l’on risque de s’encombrer de propriétés qui ne sont pas particulièrement pertinentes pour obtenir la qualité du son souhaitée. Une autre possibilité est de partir de la machine. Cette méthode consiste à créer un algorithme le plus économique possible en variables, opérations, etc. qui peut être associé à l’objet de référence. Cette démarche va à la rencontre de l’autre et " par ailleurs, elle pose plus explicitement le problème de la représentation des objets à l’aide des processus numériques ". C’est celle-ci qui a été choisie pour réaliser les algorithmes de CORDIS ANIMA.
" Nous cherchons à réaliser un processus dont la structure est permanente, capable d’évoluer de lui-même mais aussi sous l’influence d’un phénomène extrinsèque ". Ce processus, c’est l’instrument capable de vibrer seul après une excitation ponctuelle ou de répondre à une excitation continue. La suite des états de l’objet sera représentée par une suite de valeurs chiffrées, calculées, issues de l’algorithme. Le principe d’économie consiste ici à utiliser pour chaque état, les valeurs utilisées lors des états précédents pour ne pas avoir à en créer d’autres, d’en utiliser le moins possible pour économiser la place nécessaire au stockage de ces valeurs, et de les tirer des états passés les plus proches pour ne pas avoir à les stocker longtemps. Le paradigme des suites récurrentes s’impose naturellement pour traduire un tel processus.
Cependant, les valeurs des états précédant et les paramètres venus de l’extérieur (actions de l’opérateur) ne sont pas suffisants pour obtenir des phénomènes variés. Il faudra donc introduire des paramètres algorithmiques que l’on réunit sous le terme de filtre numérique27.
Une première forme de calcul, linéaire, permet de décrire les composants de catégorie linéaire. Les formules établies permettent d’englober les comportements mécaniques fondamentaux comme le point fixe, le ressort, le frottement, l’inertie, l’oscillateur harmonique. Dans un souci de simplification, la matière est concentrée dans des points matériels et donc assimilée à des masses ponctuelles, les éléments de liaison régissent uniquement les interactions entre ces points et sont assimilés à des liaisons mécaniques idéalisées. Les trois éléments fondamentaux de CORDIS ANIMA sont donc, le ressort, le frottement et la masse. Ils peuvent être réduits à seulement deux entre regroupant le ressort et le frottement dans un module de liaison mécanique. Voici la représentation de ces deux types de modules (voir Figure 14) :
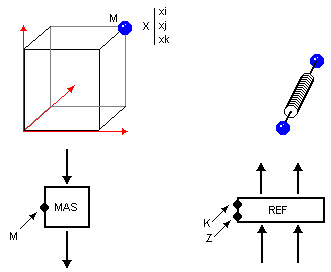
Figure 14 : Représentation des deux modules physiques élémentaires (masse et module de liaison mécanique), leur introduction dans le formalisme et leurs paramètres contrôlables : M=masse, X=vecteur position, K=constante de raideur du ressort, Z=constant
Les seuls éléments présentés jusqu'à maintenant n’offrent que des possibilités limitées et il est nécessaire de faire intervenir des non-linéarités dans l’objet physique : " si le dispositif global est rigoureusement linéaire, on ne peut espérer, par exemple lui faire produire des vibrations sonores à partir d’actions gestuelles puisque celles-ci sont par essence non-audibles ". De plus un objet constitué de composants uniquement linéaires serait monolithique.
L’organisation, en structures à trois dimensions, des éléments énoncés précédemment introduit déjà une première forme de non-linéarité. En outre les contrôles structurels et paramétriques dynamiques offrent deux autres catégories de non-linéarités. Pourtant, certains phénomènes spécifiques, comme la relation qui s’instaure entre la corde et le crin d’un archet, ne peuvent être modélisés à l’aide de ces seules ressources. C’est pour cette raison que, dès les premières versions de CORDIS ANIMA, la notion de liaison conditionnelle a été introduite. Celle-ci permet en outre de considérer des morceaux distincts susceptibles d’interagir entre eux, autant pour les objets visibles animés que pour les objets audibles manipulés.
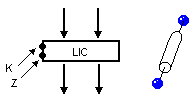
Figure 15 : Liaison conditionnelle et ces paramètres contrôlables : K=constante de raideur du ressort, Z=constante de frottement.
La liaison conditionnelle (voir Figure 15) est une liaison du type ressort-frottement recevant en entrée deux variables : la constante raideur K du ressort et la constante Z de frottement. Des conditions établies au préalable déterminent l’état de cette liaison conditionnelle en fonction des valeurs reçues en entrée. Il suffit donc, pour modifier la liaison, de modifier K et Z. Le cas le plus simple est l’annulation des variables qui permet de " couper " la liaison mais de manière générale, on affecte une valeur à K et Z parmi un ensemble prédéfini.
" La liste de conditions n’est pas limitée. Plusieurs conditions différentes peuvent faire passer dans un même état. Plusieurs conditions peuvent être vérifiées qui ne conduisent pas au même état ; dans ce cas, c’est la première rencontrée qui l’emporte. Enfin si aucune condition n’est vérifiée, il n’y a alors pas de changement d’état. "
La base algorithmique du premier système CORDIS ANIMA implanté et utilisé pour la simulation depuis presque vingt ans est ainsi constituée de ces trois éléments : masse ponctuelle, liaison ressort-frottement et liaison conditionnelle. Elle est complétée par des modules constituant une variante de ces trois derniers et introduisant une certaine souplesse dans la simulation . Les premiers modules complémentaires sont les modules dits " dégénérés ". Ces modules incomplets servent une cause pratique. Par exemple, le module SOL reçoit une somme de forces en entrée (points M) pour ne fournir qu’une position obstinément fixe en sortie : il simule un point d’attache. Un autre type de module complémentaire est constitué par " intégration " de plusieurs modules élémentaires. En effet certaines structures, comme une corde par exemple, sont constituées d’une multiplicité d’éléments semblables. Il est alors inutile voire encombrant de disposer du degré d’atomicité que nous fournissent les trois composants fondamentaux dans la mesure ou l’on peut regrouper les algorithmes définissant chaque atome en un seul, moins complexe, et plus économique.
Toute cette base algorithmique fait l’objet d’extensions, en effet, CORDIS ANIMA est conçu pour que des améliorations constantes, des compléments, puisent être ajoutés autour de cette base, afin de pouvoir obtenir n’importe quelle simulation souhaitée. Il va de soi que la variété et le nombre de ces extensions peuvent être infinis, pourtant nous tenterons de donner un léger aperçu des extensions les plus importantes.
La pratique a montré que des extensions des éléments décrits précédemment étaient nécessaires pour optimiser le principe d’économie. Ainsi la liaison conditionnelle donne naissance à la liaison conditionnelle généralisée qui permet de définir les états de la liaison non plus uniquement par les paramètres appliqués mais par des algorithmes spécifiques. Ces derniers restent compatibles avec la notion d’élément de liaison et le nombre d’états possibles reste faible (2 ou 3).
Les modules intégrés engendrent un deuxième type d’extension : les modules à " grande intégration ". Ceux-ci peuvent permettre de modéliser des éléments complexes mais homogènes d’un instrument de musique, comme par exemple une corde, un marteau ou une caisse de résonance qui ont la propriété d’être " le siège individuellement de phénomènes à variable d’état de grande dimensionnalité, mais qui sont liés entre eux par des connexions à faible dimensionnalité28 ". Autrement dit, ces structures vibrantes sont composées d’un grand nombre d’éléments identiques communiquant avec leur environnement par un faible nombre de points. Parmi ces modules à grande intégration on peut citer par exemple " la chambre modale " ou " l’agglomérat ".
Les modules " ad-hoc " constituent le troisième type d’extension le plus courant. Celui-ci est un module dans lequel tout est permis du point de vue logarithmique avec néanmoins les restrictions suivantes : sa fonction doit rester mécanique, il doit correspondre à un modèle physique et présenter un certain nombre de point de communication et d’éventuels paramètres de contrôle. Ce module permet d’intégrer à CORDIS ANIMA des démarches de modélisation de différentes natures comme les modèles de Karplus / Strong ou les guides d’ondes de Julius Orion Smith. Il convient de ne pas confondre cette ouverture vers d’autres démarches avec les modules à grande intégration décrits précédemment, ni avec les modules extra-physiques que nous allons décrire maintenant.
Ces modules extra-physiques sont des modules pour lesquels on ne cherche aucune référence à des processus physiques réels.
" Les modules extra-physiques (…) doivent précisément permettre d’introduire dans le corps même de l’objet central, des processus (…) répondant d’une autre logique que celle de la mécanique, de l’instrumentalité physique du monde ".
Toutes les extensions apportées à CORDIS ANIMA permettent d’ouvrir le système et de le développer. Néanmoins, ces modules en question sont bien délimités à l’intérieur du formalisme global de l’objet simulé.
" Cette attitude permet d’identifier rigoureusement l’emplacement des îlots non physiques et par la même, d’une part de circonscrire leurs effets indésirables, d’autre part d’exploiter leurs effets intéressants ".
Un des enjeux essentiels de Cordis-Anima est de reconstituer le rapport existant entre l'instrument et l'instrumentiste. La communication instrumentale est visuelle, auditive et tactile, et seule l'union de ces trois canaux permet une bonne perception sonore. En effet, de nombreuses expériences psychoacoustiques mettent en évidence que la compréhension du son, dans certaines circonstances, n'est possible qu'avec la participation du visuel et du gestuel. Une approche uniquement acoustique du son ne peut-être complète, Cordis-Anima intègre donc le fonctionnement de la communication instrumentale (voir Figure 16) dans sa synthèse par modèles physiques.

Figure 16 Schématisation d'une communication complète entre instrument et instrumentiste.
La réalisation d'un tel système nécessite la présence de trois interfaces. L'interface acoustique est, comme dans toute synthèse sonore, un complexe de haut-parleurs, sachant que de manière interne la structure vibrante est écoutée au moins en un point. L'interface visuelle est assurée par un écran sur lequel apparaissent les déformations de l'objet vibrant, manipulé par une interface gestuelle à retour d'effort. Cette interface est nommée transducteur gestuel rétroactif (TGR).
Exemple de deux prototypes de transducteurs gestuels rétroactifs.
Le TGR permet à la fois de communiquer au modèle le geste de l'instrumentiste, et également de renvoyer à ce dernier la réponse mécanique de l'objet. Le TGR doit se manipuler d'une façon comparable à celle rencontrée dans le monde instrumental, tout geste appliqué devra donc correspondre à un résultat sonore directement et logiquement associé, et à une réaction d'ordre kinesthésique de la part de l'instrument. Si l'instrumentiste applique une force sur le TGR, celui-ci l'enverra à un module d'excitation greffé sur l'instrument qui transmettra l'excitation à la structure vibrante modélisée. Celle-ci, mise ainsi en vibration, renverra, suivant le chemin inverse parcouru par l'information de force, sa ou ses variations(s) de position à l'instrumentiste (voir Figure 17).
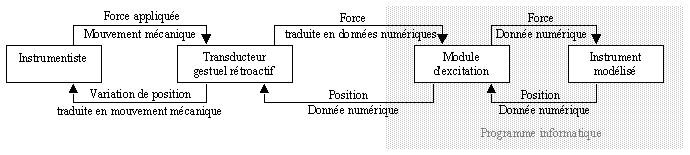
Figure 17 : Processus d'excitation avec rétroaction.
Sur ce principe, différents dispositifs ont été mis au point. Nous présenterons comme exemple, deux prototypes mis au point à l'ACROE. Le retour d'effort est ici limité à un degré de liberté.
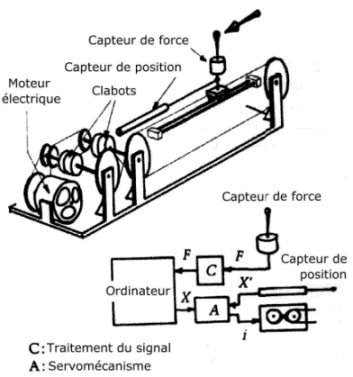
Figure 18 : Le transducteur gestuel conçu par J.L.Florens29.
Le premier appareil, conçu par J. L. Florens, en 1978, consiste en une manette montée sur un support, coulissant le long de deux guides horizontaux (voir Figure 18). Deux capteurs de pression et de position enregistrent respectivement la pression exercée sur la manette par l'opérateur et le déplacement du support le long du rail. Le retour d'effort est provoqué par un dispositif constitué d'un moteur tournant en permanence et d'un système de clabots électrodynamiques commandés par ordinateur. Le modèle simulé répond à la force exercée par retour à sa position de départ. Pour toute force appliquée, le modèle informatique calcule la réponse. Celle-ci est transmise au transducteur qui la traduit en mouvement mécanique par l'intermédiaire d'un servomécanisme et la transmet à l'instrumentiste.
Le deuxième dispositif, conçu en 1980, consiste en une touche unique inspirée de celles d'un piano, mais avec un déplacement d'une latitude de cinq centimètres (voir Figure 19). Ce système est plus complexe que le premier et fonctionne tout à fait différemment. La vibration et le bruit dus à un moteur tournant constamment sont supprimés. Le temps de réponse est plus court et la précision des mouvements est de l'ordre d'une douzaine de microns. Cependant, la moindre puissance du moteur pose problème : un obstacle parfaitement rigide est très dur à simuler. Les forces appliquées peuvent devenir très importantes en peu de temps, ce qui est difficile à modéliser sur un appareil léger et compact, limité mécaniquement. Ce prototype donnera néanmoins naissance à un clavier rétroactif breveté de 16 touches30.
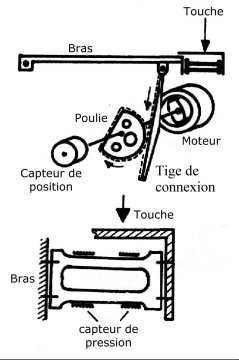

Figure 19 : Transducteur gestuel rétroactif sous forme de touche.
(a) Schéma du dispositif.
(b) Deuxième version construite en janvier 198131.
Représentation du geste et son traitement
Toute manipulation du transducteur gestuel est mémorisée sous forme de données numériques codée suivant une structuration spécifique. Ces données sont associées à des canaux gestuels différents correspondant aux différents capteurs. Le geste, pouvant ainsi être stocké sous sa représentation numérique, offre à l'instrumentiste deux possibilités de travail : soit conserver une approche purement immédiate en temps réel, soit faire appel, en temps différé, à un geste déjà mémorisé auquel cas, en vertu de sa forme purement numérique, ce dernier pourra éventuellement avoir subi quelques traitements. Ainsi, une démarche d'action en temps différé peut s'établir et offre la possibilité d'introduire toutes formes de traitements allant de la simple modification à l'application de modèles algorithmiques plus complexes (voir Figure 20).
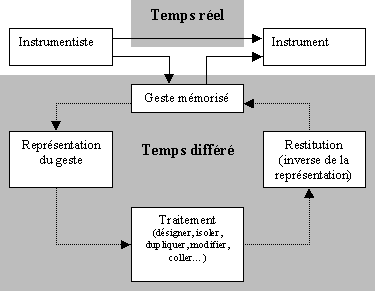
Figure 20 : Action de l'instrumentiste sur l'instrument, en temps réel ou temps différé, avec ou sans traitement du signal.
Suite à Cordis-Anima, nous allons examiner Mosaïc, autre technique de synthèse modale. Cordis-Anima est développé exclusivement à l'ACROE de Grenoble, alors que Mosaïc est développé par l'IRCAM à Paris. Cependant, les deux centres suivent de près leurs travaux respectifs, et si Cordis-Anima et Mosaïc diffèrent sensiblement malgré leur formalisme commun, la raison en est leurs objectifs distincts.
Mosaïc32 est un logiciel de synthèse modale conçu à l’IRCAM par Jean-Marie Adrien et Joseph Morrison. Il comprend un noyau composé de fonctions permettant d’exécuter les algorithmes de synthèse physique. Ces algorithmes, écrits en C++, ont été développés par Jean-Marie Adrien sur une période de plusieurs années (voir § II.3). Mosaïc à été programmé en Scheme, dialecte du Lisp, et développé sur UNIX (Dec et NeXT) puis porté sur Macintosh. Le programme comprend également un interprète du Scheme qui sert à la fois d’interface interactive et de langage d’extension. Cet interprète est le langage ELK, conçu par Oliver Laumann à l’université technique de Berlin. Les algorithmes, les mécanismes de contrôle et l’interprète du Scheme ont été intégrés au programme par Joseph Morrison.
Mosaïc8 est une boite à outils logicielle modulaire de synthèse modale qui se présente à l’utilisateur sous forme d’un établi virtuel sur lequel on place et assemble des objets en vue de créer des instruments. Ces objets sont de deux types ; il y a des objets résonnants (plaques, membranes, colonnes d’air, cordes, chevalets…) et des objets excitateurs (plectres, archets, marteaux…). Les caractéristiques de ces objets (taille, matériau…) sont précisées par l’utilisateur. Les interactions entre ces objets se font grâce à des connections représentées par des " boites noires " placées entre les objets. Elles peuvent être de différentes natures : collage, pincement, frottement, percussion, poussée… Ces connections se font à des points précis de l’objet dits points d’accès. Ces derniers peuvent se déplacer au cours de la simulation. Les différents paramètres de l’interaction, appelés commandes, peuvent être précisés. Par exemple, dans le cas du frottement d’un archet, on peut varier la vitesse de frottement, le taux de colophane, etc. Le son est généré en ordonnant au logiciel de simuler le déplacement des objets selon une trajectoire donnée, entraînant un choc, un frottement ou un autre type d’interaction avec d’autres objets. Les objets peuvent être également décrits et connectés entre eux grâce à l’interprète du langage Scheme dont nous avons parlé précédemment. Autrement dit, cet interprète, qui est lui-même un langage, permet d’écrire un petit programme décrivant l’instrument et le mouvement des objets le constituant. Il suffit alors de lancer ce programme pour que Mosaïc simule le mouvement et nous donne le son résultant.
La particularité de Mosaïc réside dans sa modalité. La vibration de l'objet simulé est décomposée en modes qui correspondent aux diverses déformations périodiques et simultanées d'un corps. Chaque mode se caractérise par un partiel (harmonique ou non) et son temps d'extinction, et est associé à une fréquence de résonance qui le met en action suivant les différents points d'excitation.
Le son de sortie est obtenu en connectant des microphones virtuels à des points d’accès de l’objet. Pour obtenir un son plus réaliste et plus proche de ce que notre oreille peut entendre dans le monde acoustique, les équipes de l’IRCAM travaillent à la réalisation d’un logiciel de calcul du rayonnement du son, ce qui permettrait de placer les microphones non plus au contact de l’objet mais dans l’espace tridimensionnel. Les travaux récents ont permis, la création d'une interface graphique conviviale pour les musiciens appelée Modalyser, sous forme d'un établi entièrement graphique, plus instinctif et dispensant totalement d’apprendre le Scheme et d’utiliser ce langage pour programmer le modèle. L'implantation du programme en temps réel par l'intermédiaire du logiciel jMax34 est encore à l'état expérimental. Des développements sont encore nécessaires pour améliorer le temps réel.
Les problèmes à résoudre sont les mêmes que pour n’importe quel autre outil de synthèse par modèles physiques : le programme doit être assez simple pour éviter les trop gros calculs, mais suffisamment complexe pour obtenir un son satisfaisant. De plus le programme se doit d’être flexible et facile à utiliser. Le premier problème est résolu par les algorithmes de Jean-Marie Adrien. Le principe de la représentation modale et le calcul pas à pas du modèle simulé permettent une obtention rapide des résultats, de plus, ils permettent de générer n’importe quel modèle aussi délirant soit-il. Le second problème ne se résout en revanche pas aussi facilement. En effet, lorsqu’on utilise Mosaïc, il faut créer l’instrument mais également en jouer, spécifier les gestes avec un haut niveau de détail. Hors, qui connaît la valeur physique de gestes que l’on réalise instinctivement ?
" What is the right lip pressure to apply to a reed in a clarinet ? Even more difficult, what is the lip pressure for an instrument that vaguely resembles a clarinet but that you have invented ? (Perhaps the instrument is 10 metres long and requires a super-human lip pressure !)35 "
La mesure des valeurs physiques sur des instruments réels permet de résoudre ce problème mais encore faut-il savoir comment réaliser une phrase musicale. La quantité d’ordres nécessaires pour indiquer à Mosaïc comment jouer musicalement une phrase est énorme, de plus, la réaction de l’instrument dépend de l’action précédente à laquelle il a été soumis. Il est donc nécessaire de synchroniser les actions pour rendre la phrase musicale cohérente.
Il est évident que seul le créateur est à même de décider la façon dont l’instrument qu’il a créé doit être joué. Comme Adrien et Morrison le signalent avec humour, il peut décider que la façon normale de jouer de la guitare est de frapper le dos de la caisse avec des mailloches. Cependant, une bibliothèque de connaissances permettant de résoudre les problèmes acoustiques courants constituerait une aide non négligeable pour la simulation d’instruments inventés. Mosaïc est un programme ouvert dans le sens ou cette bibliothèque peut être constituée au fur et à mesure, en isolant les programmes simulant une interaction satisfaisante musicalement et en les stockant séparément, dans le but de les réutiliser plus tard. De nouveaux objets résonnants ou excitateurs peuvent également être ajouté aisément au programme. Des objets déjà complexes comme une touche de piano, par exemple, peuvent être stockés sous un nom donné, de manière à être réutilisés dans une machine encore plus complexe sans qu’il soit nécessaire de réécrire toute cette partie du programme.
Mosaïc n’est pas seulement un outil de synthèse par modèles physiques, les enjeux réels de ce programme sont clairement décrits par j. D. Morrison et J.-M. Adrien.
" MOSAIC may be viewed as a "physical synthesis sound description language", in much the same way PostScript is considered a printed page description language. Though PostScript is itself a powerful programming language, it is rarely used for programming by human ; far more often it is used as an output language for drawing programs. Similarly, it is expected that in the future, users will rarely program directly in MOSAIC ; rather, they will use higher level interfaces that use MOSAIC as an output language36. "
Les objets
Il existe plusieurs méthodes pour obtenir les structures complexes chargées d’émettre des sons. Premièrement, il est possible d’utiliser les objets37 proposés par Mosaïc pour construire un instrument simple et homogène. Ces objets sont les cordes, les barres, les modèles à une masse ou deux masses, les tubes (fermés à un ou aux deux bouts), les membranes circulaires ou rectangulaires (d’épaisseur nulle), les plaques circulaires ou rectangulaires (d’épaisseur non-nulle) libres ou fixes, et les chevalets de violon ou de violoncelle. Pour chacun de ces objets il est nécessaire de spécifier les paramètres comme la longueur, l’élasticité, la matière, etc.
Voici par exemple les lignes du programme permettant de créer une corde38 :
| (define my-string | =>je définis la chose appelée " my-string" |
| => j’en fais un objet de type corde | |
(length .5) (tension 150) (density 1000) (radius .001))) |
=>je définis ses paramètres : mode vibratoire, longueur, tension, densité, rayon (à la section) |
La deuxième solution est d’obtenir la structure par une méthode extérieure à Mosaïc : par une analyse expérimentale, par une analyse informatique d’éléments finis ou toute autre technique.
La troisième et dernière façon d’obtenir l’instrument de musique souhaité est de créer un hybride entre deux structures déjà existantes. Il existe deux types hybridation : le fondu (melt) ou le mélangé39 (mix). Dans l’hybride final, La proportion de chaque structure peut-être variée dynamiquement. Dans un hybride fondu, les caractéristiques des deux instruments sont intimement mêlées, les deux instruments ne forment plus qu’un. Si par exemple on hybride de cette manière une corde longue et une corde courte, l’hybride, une fois excité, produira un son plus aigu ou plus grave selon la proportion de chaque structure présente dans celui-ci. En revanche, l’hybride mélangé se contante de " coller " ensemble les deux objets. L’hybridation des deux cordes aboutirait dans ce cas à un instrument laissant entendre les deux sons des deux cordes. La puissance respective du son de chaque corde dépendra de la proportion de chacune d’elles dans l’hybride.
Connexions : actions et interactions
Mosaïc propose un certain nombre d’interactions ( pré-programmées) possibles entre les objets. Par exemple, on peut choisir d’établir une interaction du type " frappement " entre une barre de bois et une plaque de métal. Pour faire interagir deux objets, il est nécessaire de choisir un point d’accès sur chacun d’eux, c’est à dire : le point qui doit rentrer en contact avec l’autre objet. L’interaction se place alors entre ces deux points d’accès comme une boite noire indiquant une relation entre eux (voir
![]()
Figure 21 : Modèle d’interaction entre deux objets.
Collage (adhere) : Cette action permet de coller le point d’accès d’un objet à celui d’un autre objet. Elle est utilisée pour assembler les différentes parties d’un instrument. Dans cet exemple, deux cordes sont " collées " par l’intermédiaire de deux points d’accès40 :
| (define acc1(make-acces string1 (const .6) trans0)) | ||
| => je définis la chose appelée "acc1", j’en fais un point d’accès placé sur l’objet "string1" que j ‘ai défini au préalable | ||
| (define acc2(make-acces string2 (const .4) trans0)) | ||
| => je définis la chose appelée "acc2", j’en fais un point d’accès placé sur l’objet "string2" que j ‘ai défini au préalable | ||
| (make-connection ‘adhere acc1 acc2) | ||
| => je crée une connexion de type collage entre les deux points d’accès "acc1" et "acc2" | ||
Frottement (bow) : Cette fonction n’exécute pas directement un frottement entre deux objets. Les points d’accès des deux objets sont en contact et c’est seulement lorsqu’un mouvement et appliqué à l’un des deux objets que le frottement à lieu.
Pincement (pluck) :Une fois encore le pincement n’a lieu que si l’un des objets est mis en mouvement. Le point d’accès de l’objet pinceur " agrippe " le point d’accès de l’objet pincé mais lorsque les objets sont éloignés l’un de l’autre, un maximum de tension (défini par l’utilisateur) est atteint et la connexion entre les deux point d’accès est rompue : le pincement à lieu.
Anche simple (simple reed) : Cette interaction à été spécialement crée pour facilité la conception d’instruments à anche. Un des points d’accès est considéré comme un point d’une anche et l’autre comme un point d’un tube acoustique. De nombreux paramètres permettent de définir les flux d’airs. Il faut remarquer que cette interaction fonctionne également avec n’importe quels autres objets, cependant le son obtenu n’est pas le son typique d’un instrument à anche.
Frappement (strike) : Dans le cas où un mouvement est imprimé à l’un des objets, un frappement à lieu entre eux. Il est possible d’effectuer toute une série d’interactions de frappement entre deux objets dans le but de simuler leur proximité et l’éventualité d’un contact entre eux.
Etranglement ou Touche (neck or fingerboard) : Cette connexion est conçue tout spécialement pour simuler la présence d’une touche sur un instrument à cordes comme le violon. Un objet et utilisé pour pincer la corde, leur points d’accès sont en contact, et la présence simulée de la touche, permet de bloquer la corde afin de diminuer sa longueur vibrante. Si cette " touche " virtuelle était absente, on obtiendrait le même effet qu’en posant le doigt sur la corde d’un violon sans la plaquer contre la touche.
Il est intéressant de remarquer que la définition de ces interactions ne tient pas compte de la nature des objets qui interagissent entre eux. Ceci est particulièrement visible dans les lignes de programmes illustrant la fonction collage (adhere). Cela implique que n’importe quels objets peuvent interagir entre eux : un tube peut servir d’archet à une corde, un corps de violon peut servir d’anche à un tube, etc. Ce genre de combinaison produit des sons bizarres mais reste physiquement cohérent.
En complément de ces fonctions définissant des interactions, il existe des actions simples applicables aux objets par l’intermédiaire d’un seul point d’accès (voir
![]()
Figure 22 : Exemple d’action sur un objet : une poussée est appliquée à la barre de bois.
Trou (tube hole) : Cette action n’est utilisable que sur un tube et simule l’ouverture d’un trou dans ce dernier.
Excitation (force) : Cette action permet d’appliquer une force sur un point d’accès avec une orientation donnée dans le but par exemple de mettre en mouvement un archet qui doit frotter une corde.
Vélocité (velocity) : Cette fonction limite la vélocité en un point d’accès donné.
Position : Cette fonction limite le mouvement d’un point d’accès donné.
Enfin, ces trois dernières connexions offrent des compléments utiles :
Micro (pick up) : La variation de la pression acoustique au point d’accès choisi est envoyée dans un fichier de son (enregistrement qui peut ensuite être écouté). Voici les lignes du programme permettant de créer une membrane, un point d’accès sur cette membrane et un micro relié à ce point d’accès41 :
| (define membrane (make-object ‘rect-membrane ‘() 24 .6 .4 111 .1 .5 .5)) | ||||
| => je définis la chose appelée "membrane", j’en fais un objet du type membrane-rectangulaire et je définis ses paramètres | ||||
| (define menbrane-listen-point (make-acces menbrane (const .7 .4))) | ||||
| => je définis la chose appelée "membrane-listen-point", j’en fais un point d’accès sur la membrane et je définis ses caractéristiques | ||||
| (make-output membrane-listen-point ‘x) | ||||
| => je crée un micro connecté au point d’accès "membrane-listen-point" | ||||
Mode mix : Cette fonction permet d’envoyer la combinaison des différents modes vibratoires d’une structure dans un fichier de son.
Dopage (dope) : Cette connexion permet d’ajouter une excitation extérieure (signal audio) à la vibration d’une structure spécifique, durant la simulation. Il est par exemple possible d’exciter un gong avec la vibration d’une voix parlée.
Les contrôleurs
Les contrôleurs sont des fonctions utilisées pour spécifier les valeurs qui sont susceptibles de varier dans le temps. Il ne faut en aucun cas les confondre avec les paramètres associés à chaque objet, dont le rôle est de définir leurs caractéristiques (longueur, densité…). Pour comprendre le rôle de ces contrôleurs il suffit d’imaginer que la machine simulée par Mosaïc est une boite noire sur laquelle se situent des boutons, un pour chaque contrôleur. Les boutons correspondant à des contrôleurs constants sont collés à leur place et ne peuvent pas être bougés. Les boutons correspondants à des contrôleurs d’enveloppe suivent cette enveloppe dès que la machine est mise en marche.
Ces contrôleurs n’ont pas uniquement pour rôle de transmettre des valeurs, mais peuvent également en recevoir : ils possèdent une sortie et peuvent avoir une ou plusieurs entrées. Ceci permet de créer de véritables réseaux de contrôleurs, et de produire un système de synthèse FM42 ou de synthèse additive43.
Mosaïc propose plusieurs contrôleurs pré-programmés qui apportent une flexibilité supplémentaire au système :
Constant : Ce contrôleur génère une valeur constante ce qui est pratique lorsque l’utilisateur doit obligatoirement utiliser un contrôleur mais qu’il ne désire pas faire varier la valeur.
Enveloppe (Breackpoint enveloppe) : la valeur de sortie de ce contrôleur suit une enveloppe indiquant la valeur limite acceptable.
Générateur de fréquence (Sine generator) : Ce contrôleur délivre une onde sinusoïdale dont la fréquence doit être spécifiée par un autre contrôleur branché en entrée.
Fichier MIDI (MIDIfile) : Ce contrôleur permet d’utiliser des fichiers MIDI comme source de données. Il extrait les valeurs intéressantes et les transmet en sortie.
Dernier échantillon (Last sample) : Ce contrôleur permet de réutiliser le dernier échantillon de son produit par la machine simulée, dans le but par exemple, de créer une rétroaction.
Echelle (Scale) : Ce contrôleur permet d’effectuer un changement d’échelle. En entrée, il reçoit les valeurs d’un autre contrôleur (entre 1 et 100, par exemple) et les met à l’échelle souhaitée (entre 1 et 20, par exemple) avant de les communiquer en sortie.
Dynamique (Dynamic) : Les contrôleurs dynamiques sont similaires aux contrôleurs constants, mais ils ont la particularité de pouvoir être contrôlés en cours de simulation. Dans le programme lui-même on peut insérer des lignes de commande pour changer la valeur de ce contrôleur. Les valeurs correspondant à l’analyse d’une exécution instrumentale réelle peuvent être envoyées à de nombreux contrôleurs dynamiques qui contrôleront le jeu de l’instrument virtuel simulé.
Universel (Universal) : Ces contrôleurs universels peuvent être programmés à volonté par l’utilisateur Ils peuvent contenir des fonctions arbitraires en Scheme mais ils ne doivent pas être utilisés en trop grand nombre car ils ralentissent la synthèse du son.
Toutes ces actions, interactions et contrôleurs, sont présents dans Modalys sans grandes modifications. Modalys présente en revanche plusieurs améliorations que nous allons détailler maintenant. Nous évoquerons également Modalys-ER, l'interface graphique développée pour Modalys.
Modalys10 est, comme nous l’avons dit précédemment, le successeur de Mosaïc. Les travaux de recherche et le développement du système ont été repris à l’IRCAM en 1994 par l’Equipe de Recherche en Acoustique Instrumentale dirigée par René Caussé et l’équipe de développement des interfaces et de la représentation du son dirigée par Gerhard Eckel. La nouvelle version du programme, renommée Modalys pour éviter toute confusion avec le navigateur Internet nommé Mosaïc, à été portée sur de nombreuses plates-formes informatiques et est désormais disponible sur DECStation, DECAlpha, NeXT, SGI, Macintosh et PowerMacintosh. Comme la première version du programme supportait mal les accès directs aux données modales, la nouvelle version comprend une palette de modules de contrôle pour la manipulation de données modales statiques ou dynamiques. Ce système permet au compositeur de contrôler avec finesse les données modales, en accord avec ses besoins. Aujourd’hui Modalys s’est associé avec le programme Modalyser, interface graphique conviviale, mise au point à l’Université du Hertfordshire en Grande-Bretagne, et porte le nom de Modalys-ER.
Les travaux en cours s’orientent vers l'implantation de Modalys en temps réel. Un accès totalement en temps réel faciliterait le contrôle du modèle car il deviendrait possible de modifier les paramètres en cours d’écoute du son, grâce à des manettes, pédales d’effets, claviers, contrôleurs de souffle, etc. La version disponible en temps réel sur jMax et Max/MSP pose encore de nombreux problèmes. Le procédé est très coûteux en temps de calcul, seules des structures très simples peuvent être simulées et le nombre de modes (d'harmoniques) calculés pour chaque son doit être très réduit. Les optimisations en cours portent donc sur la vitesse de calcul qui permettrait d'augmenter le nombre de structures simultanées simulées et le nombre de modes pour chaque son. La solution pourrait venir de l'utilisation de la technique " multi-threading ". Cette méthode consiste à utiliser plusieurs processeurs (au moins deux) qui se partagent les tâches. Un des processeurs calcule le modèle à part, et quand il a fini, communique ses données au deuxième processeur qui met la nouvelle configuration en service. Ce procédé permet d'éviter les " clics ", ainsi que le retard dans le calcul des échantillons de son.
Lors des journées d'informatique musicale du forum de l'Ircam qui se sont déroulées du 8 au 10 mars 2000, il a été possible d'assister à la simulation en tant réel d'une corde excitée tantôt par une masse et tantôt par le son d'une voix captée par un micro. Le dispositif tournait sur un Pentium II à 450 MHz. En demandant à la machine de calculer 20 modes avec deux excitateurs (la masse et la voix), 30% de la capacité de calcul de la machine étaient utilisés. L'augmentation du nombre de modes ou le déplacement de l'excitateur augmentait considérablement ce pourcentage. Aucune simulation d'hybride entre deux structures n'était possible. Autre élément curieux : un déplacement de la masse au contact de la corde donnait un son granuleux comme si la corde avait été striée. Ceci est dû à la discrétisation de la corde.
Un éditeur en trois dimensions basé sur le langage Java est en cours de création, à l'université du Hertfordshire.
Les deux grandes techniques à vocation musicale, Cordis et Modalys, que nous venons d'évoquer, ne sont pas les seules à avoir fait l'objet de compositions musicales. La synthèse par guide d'ondes, qui s'appuie sur un formalisme totalement différent, a, elle aussi, su séduire les compositeurs, et ceci en raison son caractère économique en puissance machine et en temps de calcul.